|
Glossary Activity The activity of a sample is defined as the number of decays in a unit of time. (The time-unit should be much shorter than the half-life).
The unit of the activity in the SI system is: becquerel
Denoted by: Bq
1 Bq = 1 decay/s. The activity of a sample is proportional to the number of the nuclei N in the sample and to the decay constant 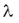 . . 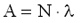
Since the number (N) of the radioactive nuclei in a sample follows the exponential decay law, the activity of the sample is also decreasing at the same rate. Decay constant The decay of radioactive materials is a random process. The probability that a particular nucleus will decay in a unit of time (e.g. 1 s) is called decay constant. The decay constant is usually denoted by : 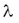 The unit of the decay constant is (in SI units): 1/s. Small value of the decay constant results in slow decay, large value of the decay constant results in fast decay. If the decay constant is known, the activity of the material can be determined by the expression: 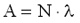
Here A represents the activity of the material (number of decays in a unit of time), N is the number of the radioactive nuclei in the sample. The decay constant is also related to the half-life: 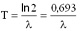
T is the half-life of the sample. Half-life The amount of time necessary for the half of a parent isotope to turn into its daughter isotope is called half-life. The expected number of nuclei N(t) in function of time (t) can be calculated by the following mathematical expression. 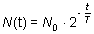
Here t denotes the time, N0 is the number of nuclei at the beginning (t=0) and T is the half-life. The function is shown below in the graph. 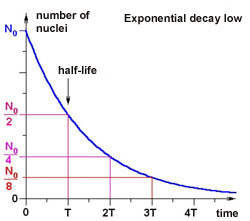
The half-life and the decay constant are inversely proportional to each other: the smaller is the decay constant, the more time is required for the decay of the half of the sample. 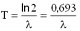
Here T is the half-life, 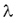 is the decay constant. is the decay constant. The half-life is characteristic of the isotope. The half-life of the different radioactive materials can range from several billion years to billionth of a seconds. The probability that a particular nucleus decays during T1/2 time (T1/2 is the half-life) is exactly 1/2. The decay probability during the next T time period is again 1/2, and it is independent since how long the particular nucleus is “waiting” already for the decay.
|








