Egy dimenziós húrra befogott elektron állapotfüggvényei

A húrra befogott elektron az egyik legegyszerűbb modell, amin a kvantummechanika alapjai bemutathatók. Középiskolában – érthető módon – csak valós függvényekkel számolnak, és így egy okos, érdeklődő tanuló több kérdésére is nehéz választ adni. Ilyen kérdések a következők:

• A hullámfüggvényt egy megrezgetett kötélhez szoktuk hasonlítani, és a függvény négyzete mutatja meg, hogy „hol van” az elektron (megtalálási valószínűség). Van azonban olyan pillanat a rezgés során, amikor a kötél kitérése mindenütt nulla. Hol van ilyenkor az elektron? Eltűnt?

• A hullámfüggvény rezgésének a frekvenciáját ismerjük az E=h∙f alapján. Ha az elektron is így rezeg, akkor sugároznia kell, mint egy antennának. Miért nem sugároznak folyamatosan a „rezgő” elektronok az atomi állapotokban? (A válasz az, hogy az elektron „áll”, csak a függvény rezeg.)

• Hogy van az, hogy a hullámfüggvény rezeg, az elektron pedig "áll" az atomi állapotokban?

• Hogyan tud egy elektron EM hullámokat kibocsátani vagy elnyelni? Úgy viselkedik ilyenkor, mint egy antenna? Ezt hogyan tudja megtenni, ha minden atomi állapotban "áll"?

Ez a szimuláció segítséget ad ezeknek a kérdéseknek a megválaszolásához.

Rövid elméleti összefoglaló

A kvantummechanika szerint egy egydimenziós húrra befogott elektron állapotfüggvénye a következő:

.

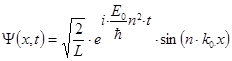Itt , ,

L a húr hossza, m az elektron tömege és n = 1, 2, 3, 4…

A középiskolában nem beszélhetünk komplex függvényekről, de mondhatjuk azt, hogy egy részecske állapotát nem egy, hanem két (valós) függvénnyel írjuk le. Nevezzük ezeket Reѱ és Imѱ–nek. Ezek olyanok, mintha egy vektor komponensei lennének. Azt, hogy éppen „hol” van a részecske a (Reѱ)²+(Imѱ)² kifejezés mutatja meg. Ez a középiskolások számára sem idegen, hiszen egy vektor hosszúságának négyzetét is a komponensek négyzetösszegeként lehet kiszámítani.

A fentiek alapján nyilván

, és .

Ez a szimuláció segítséget ad a következőkhöz:

1) Az állapotfüggvények két komponensének (Reѱ és Imѱ ) szemléltetéséhez, időbeli viselkedésükkel együtt. Az egyes állapotok időfejlődését leíró frekvencia az összefüggés alapján számítható, ahol .
A „szemléltetés” történhet a valós (Reѱ) és képzetes (Imѱ) részek külön-külön történő ábrázolásával (2D ábrázolás), de lehetőség van 3D koordinátarendszerben (x, Reѱ, Imѱ) történő ábrázolásra is.

2) Két, tetszőlegesen választott állapot egyenlő arányban történő szuperpozíciójából kialakult

állapotfüggvény 2D és 3D ábrázolására is.

3) A kevert állapothoz tartozó megtalálási valószínűség időbeli változásának megfigyelésére, és a kevert állapot „tömegközéppontjának” a meghatározására.
(Egyetlen állapot állapotfüggvényének megtalálási valószínűségét úgy lehet figyelni, hogy a kevert állapot mindkét komponenséül ugyanazt az állapotot választjuk.)

Érdekes megfigyelni

a) A sajátállapotok állapotfüggvénye időben változik, ám a tömegközéppontjuk időben állandó, így az ezekben lévő elektronok nem „mozognak”, és így nem sugároznak.

b) Egyes kevert állapotok tömegközéppontja rezgőmozgást végez. Egy rezgőmozgást végző elektron viszont „antennaként” sugároz.

c) Megfigyelhető, hogy a rezgőmozgás frekvenciája , azaz a két frekvencia különbsége (a rezgőmozgás amplitúdóját és frekvenciáját a program nem képlet alapján, hanem a kialakult mozgásból határozza meg, ezért várni kell, amíg legalább egy teljes rezgési periódus lezajlik). Figyelembe véve az összefüggést, kapjuk, hogy . Visszakaptuk a Bohr-féle eredményt a kibocsátott foton frekvenciájára.

d) Megfigyelhető, hogy csak olyan sajátállapotok szuperpozíciójánál alakul ki a tömegközéppont rezgése, amelyek szimmetriája a húr felezőpontjára nézve különböző. Így nincs rezgés az n = 1 és n = 3 kevert állapotban, sem pedig az n = 2 és n = 4 esetén. A háromdimenziós atomoknál ez az oka például annak, hogy a 2s → 1s átmenet abszolút tiltott (mivel mindkét állapot gömbszimmetrikus, így a kevert állapot is az, tehát a súlypont helyzete nem változik).